La Caracterización
La distribución t de Student es la distribución de probabilidad del cociente
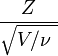
donde
- Z tiene una lateral de media nula y mediana 1
- x tiene una distribución bilateral con \nu\ grados de confianza
- o y z son independientes
Si μ es una constante no nula, el cociente  es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad
es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad  .
.
 es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad
es una variable aleatoria que sigue la distribución t de Student no central con parámetro de no-centralidad  .
.Aparición y especificaciones de la distribución t de Student
Supongamos que X1,..., Xn son variables aleatorias independientes distribuidas normalmente, con media μ y varianzaσ2. Sea
la media muestral. Entonces
sigue una distribución normal de media 0 y varianza 1.
Sin embargo, dado que la desviación estándar no siempre es conocida de antemano, Gosset estudió un cociente relacionado,
es la varianza muestral y demostró que la función de densidad de T es
donde  es igual a n − 1.
es igual a n − 1.
 es igual a n − 1.
es igual a n − 1.
La distribución de T se llama ahora la distribución-t de Student.
El parámetro  representa el número de grados de libertad. La distribución depende de
representa el número de grados de libertad. La distribución depende de  , pero no de
, pero no de  o
o  , lo cual es muy importante en la práctica.
, lo cual es muy importante en la práctica.
 representa el número de grados de libertad. La distribución depende de
representa el número de grados de libertad. La distribución depende de  , pero no de
, pero no de  o
o  , lo cual es muy importante en la práctica.
, lo cual es muy importante en la práctica.
FUENTES:
@wikipedia 2014 http://es.wikipedia.org/wiki/Distribuci%C3%B3n_t_de_Student
@matematicas visuales 2014 http://www.matematicasvisuales.com/html/probabilidad/varaleat/tstudent.html
INTEGRANTES
Julio Cesar Navarro Ballesteros
Omar Paul Monroy Navarrete
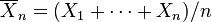





 para x>0
para x>0